图论中的最短路径问题

路径:可表示为节点序列或边的序列.

路径长度

有权图:需要考虑边的权重

无权图:边的数量

概念

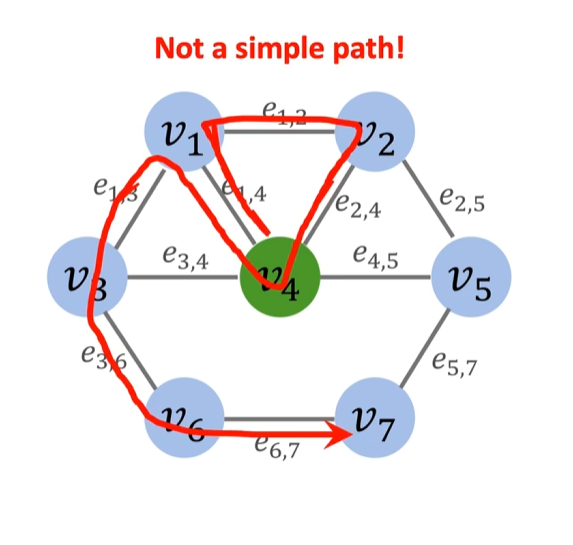
简单路径

直接通往目标节点,不会绕圈.反例如下:

最短路径

单源最短路问题:从一个节点到其他所有节点的最短路径的问题.

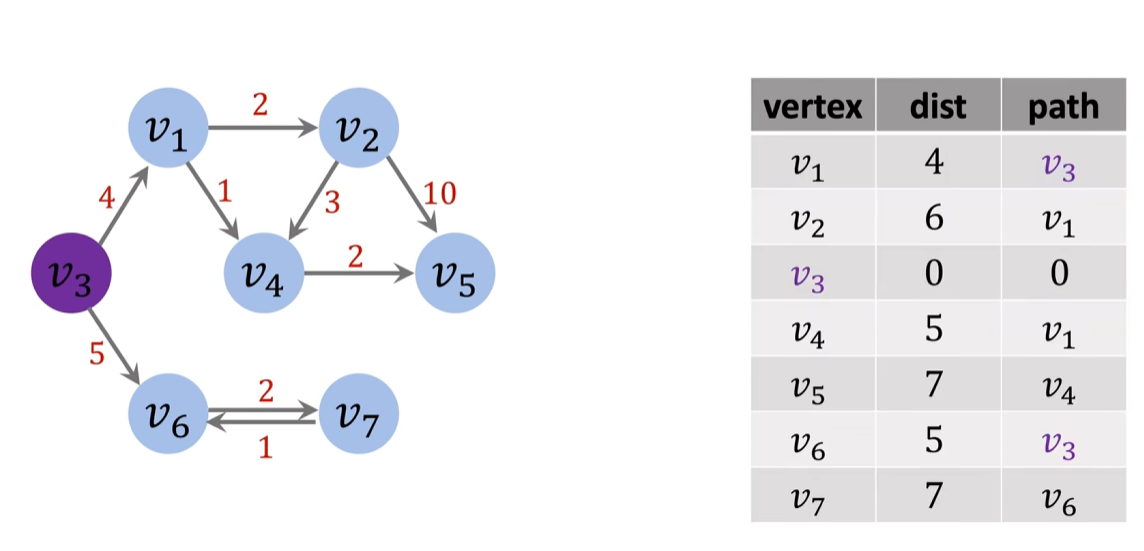
右表:从V3开始到所有边节点的最短路径长度,以及终点的前一个节点.通过一张表可以完全复原出从V3到所有节点的所有路径

路径复原:例如找到从V3到V5的最短路径,步骤如下:

找到V5所在的第5行,得知长度为7,且可得路径:V3->…->V4->V5,V5的前置节点是V4
找到V4所在第4行,可得路径:V3->…V1->V4->V5,V4的前置节点是V1
找到V1所在第一行,可得路径V3->V1->V4->V5,V1的前置节点是V3

则可知路径为V3->V1->V4->V5,长度为7.

无权图的最短路径算法

条件: 无权图,边的权重都是1,不可到达记为正无穷.

Algorithm算法:

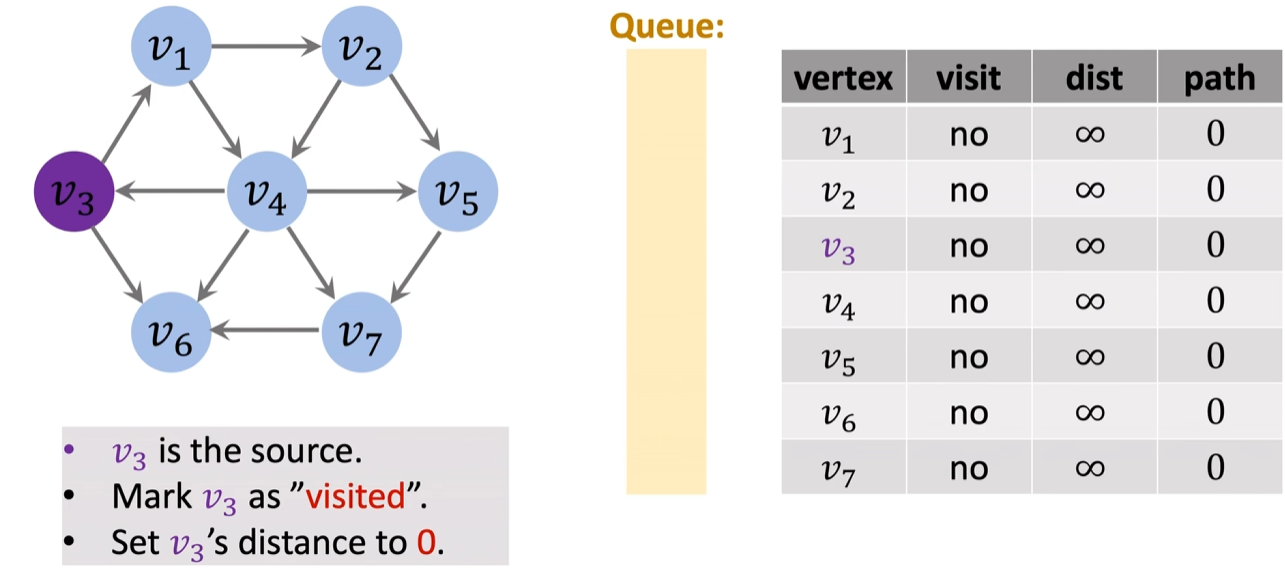
输入数据:一张图和一个起始节点

输出:一张单源最短路的表.(如上图右表).

算法描述:

初始化表:

创建一张表,[节点,是否访问,距离,前置节点]

是否访问全部标记为否,距离为正无穷,前置节点置0

将V3标记为已经被访问

V3入队,此时队列中只有V3

标记V3到节点(目前是V3)的距离为0,记为dist

进入循环(以第一次循环为例)

队首元素出队,若队列为空,则结束循环,返回结果(第一次是v3,之后是上次循环入队的元素)

找出与v3有边相连的所有出节点,如果没有,直接忽略(v1,v6)

处理队列中的节点(第一次循环时为v1,v6){

节点(v1或V6)是否被访问过?//如果已被访问,则表明之前的访问路径比本次访问更短,故不作操作

是:不做处理,忽略节点,进入下一次循环

否:{

节点(V1或V6)入队

标记节点(v1或V6)已被访问,写入表中

dist+1,写入表中

v3到v1(或V6)的路径记为v3(即V1(或V6)的前置节点),写入表中

	}
}

对于无向图,可视为所有的边都有是双向,即每次循环不仅仅只遍历出节点,入节点也要被处理

有权图中的最短路径问题

条件: 有权图,边的权重都不唯一,不可到达记为正无穷.

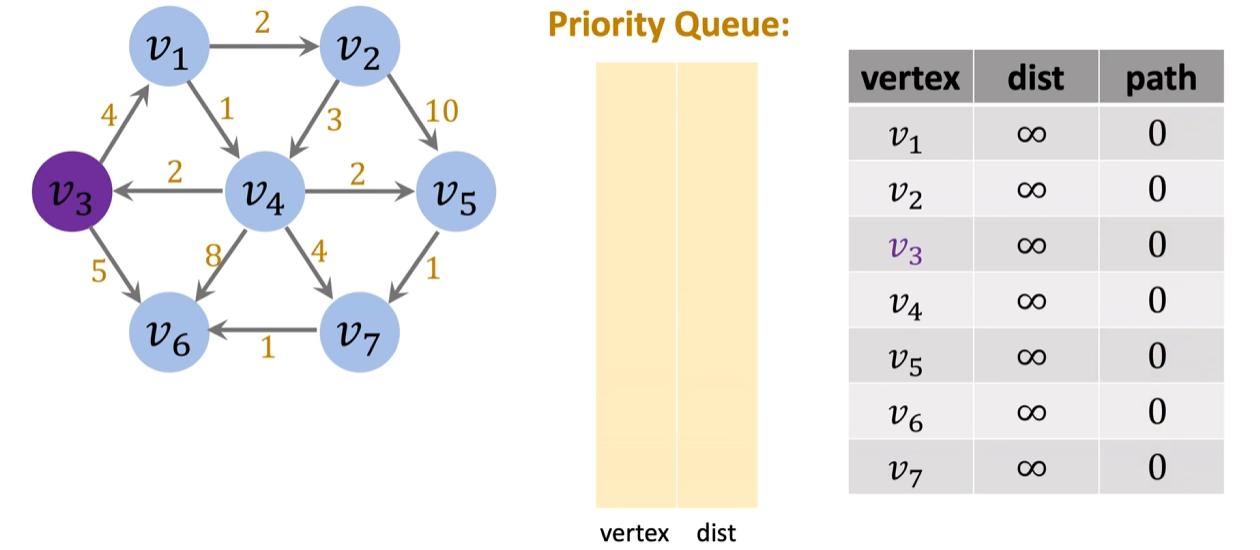
Dijkstra算法(迪杰斯特拉算法)

**要求:**所有边的权重>=0,否则会陷入无限循环.

输入数据:图,起始节点

输出数据:表[节点,距离,路径]

初始化

创建两个队列vertex和dist(称之为优先队列,距离越小优先级越高,即距离越小越靠前),一张表[节点,距离,路径]

初始化表中所有距离为正无穷,路径是0

标记表中v3(起点)的距离是0,将V3及其距离0分别入队vertex和dist(或创建包含节点和距离的对象 ,入同一队列)

进入循环(以第一次循环为例)

{
取出队列顶端的节点({v3,0}),当前路径长度记为distance+=[当前节点.距离],若队列为空,结束循环

找到全部相邻节点({v1,4},{v6,5}),如果没有,跳过节点,开始操作下一节点

操作全部相邻节点并更新表{
	如果表中[当前节点.距离]<(distance+[当前节点.距离])({v1.∞}<{v1,4}):{
		更新表中[当前节点.距离]为distance+[当前节点.距离]//距离越近越好
		更新表中[当前节点.路径]为v3
        将当前节点按大小顺序插入队列,若队列中已存在该节点,则将其距离重新赋值//之后,当前节点下游路径会受影响当前节点影响
	}否则{
	不更新节点和表,直接下一个节点
	}
}

时间复杂度:

$T=O((v+e)\log v)$

呵呵,这块完全没学会